Microscopic theory of absorption, dispersion, and refraction of materials; classical and quantum mechanical description of optical properties.
Course Description
This course discusses the interaction of light with matter. We will find that many important optical properties can be described quite accurately using surprisingly simple models. Initially we will model atoms as classical dipole oscillators (“electrons on springs”). We will use the calculated behavior of these model atoms together with Maxwell’s equations to obtain expressions for the frequency dependent refractive index, absorption, and susceptibility. Using this theory we will be able to understand the optical properties of gases, liquids and solids, including metals, semiconductors and dielectrics. To improve on our model descriptions we will discuss the foundations of quantum mechanics, and derive a quantum mechanical description of the refractive index. We will include the interaction of light with oscillations of atoms (molecular vibrations and rotations, phonons) and consider how quantum mechanics affects molecular absorption spectra.
Prerequisite
- Graduate standing or consent of instructor
List of Topics
I. Maxwell’s Equations and the Dielectric Function:
- free charge
- vacuum displacement
- meaning of susceptibility and polarization response
- bound electron polarization and magnetization
- causality & Kramers-Kronig relations
II. Optical Properties of Solids Liquids and Gases:
- molecules
- liquids
- metals
- insulators
- semiconductors
III. Classical Treatment of Light-Matter Interaction:
- Lorentz oscillator
- Drude model
- Debye model
- calculation of susceptibility and complex refractive index
- Sellmeier equations and Abbe number
- electronic transitions in atoms
- anharmonic classical oscillator model
- second order effects
- third order effects
- molecular rotational/vibrational transitions in molecules
- dipole-active and Raman-active modes
- phonons in solids
- acoustic modes
- optical modes
IV. Quantum mechanical description of light matter interaction:
- wavefunctions
- Eigenfunctions
- orthonormal complete sets
- Operators
- Dirac notation
- observables, commutation
- ensemble averages
- energy Eigenfunctions
- time independent Schrödinger equation
- infinite and finite wells, barriers
- time dependent Schrödinger equation
- time dependent perturbation theory
- Fermi Golden Rule
- expectation value of Polarization, susceptibility
- oscillator strength
- dopants / impurities in dielectric hosts
- Kronig-Penney Model and Energy bands
- Band gaps, Excitons, impurities (n- and p-type)
- blackbody radiation
- Einstein coefficients
- Thermal distributions (Bose-Einstein, Fermi-Dirac, Maxwell-Boltzmann)
Learning outcomes
Students will be able to identify materials based on reflection, transmission, absorption spectra, predict optical properties based on dopant concentrations and resonances, predict refractive index spectra based on absorption spectra, understand the role of quantum mechanics in optical properties.
Recommended reference texts
- Optical Properties of Solids. M. Fox (Oxford University Press)
- Quantum Mechanics for Scientists and Engineers. D. A. B. Miller (Cambridge)
Optional reference texts
- Optical Materials. J. Simmons and K. S. Potter (Academic Press)
- Introduction to Solid State Physics. C. Kittel (Wiley)
- Optical Electronics in Modern Communications A. Yariv (Oxford)
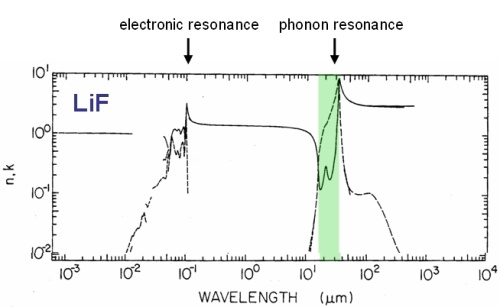
Real and imaginary refractive index a lithium fluoride (LiF) crystal