In collaboration with Dr. Bandres (CREOL) group
Stable resonator cavities can support, apart from the fundamental Gaussian beam, three different fundamental families of transverse modes: the Hermite Gaussian modes (HGM) in Cartesian coordinates, Laguerre Gaussian modes (LGM) in cylindrical coordinates, and Ince Gaussian modes (IGM) in elliptical coordinates. These three fundamental families of modes of spherical stable resonators, the HGM, LGM and IGM, are of paramount significance. Besides being the modes of the most elemental laser cavity, they are key in our understanding of more complex cavities, beam propagation, and most importantly, they serve as the foundation of structured light.
One can generate modes that closely resemble nondiffractive or accelerating beams directly from a spherical stable resonator under the right conditions. Therefore, considering the significance of the fundamental families of modes in spherical laser resonators, an intriguing question arises: is it possible to find a new family of lasing modes?
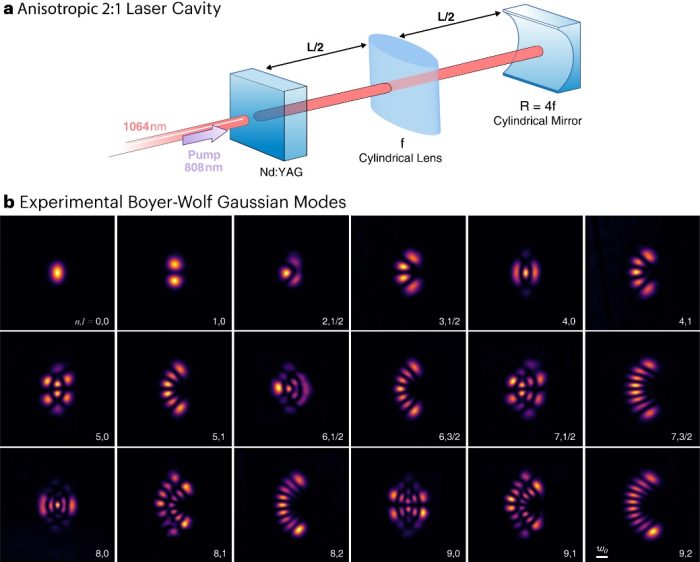
We experimentally demonstrate a new family of fundamental laser modes of stable resonators: the Boyer-Wolf Gaussian modes. By studying the isomorphism between stable laser resonator cavities and quadratic Hamiltonians, we designed a laser resonator equivalent to a quantum two-dimensional anisotropic harmonic oscillator with a 2:1 frequency ratio. The Boyer-Wolf Gaussian modes emerge in a parabolic coordinate system and are constructed by a product of solutions to the sextic anharmonic oscillator. Due to their inherent parabolic symmetry the Boyer-Wolf Gaussian modes break the symmetry around the y-axis that is present in the HGM, LGM, and IGM, and create a dark parabolic region around the x-axis.