Conventional head-up displays (HUDs) suffer from a limited exit pupil and a lack of compactness mainly due to the use of bulky optics. HUDs need a high-quality image with a large field of view (FOV) in small packaging to gain commercial acceptability. Holographic HUDs are phase-only devices that allow vision correction and focus adjustment while having a wide FOV. However, the limited bandwidth of a spatial light modulator (SLM) imposes a trade-off between the FOV and eye-box size. Combining a holographic system with an image-replicating element eliminates such a tradeoff. For image replication, we designed and fabricated a compact 2D diffractive beam splitter formed from two perpendicular volume gratings operating in the Raman-Nath regime. The gratings were recorded holographically in photo-thermo-refractive (PTR) glass, with optimized index modulation, thickness, and period to provide uniform intensity distribution across all desired orders for the fundamental red, green and blue (RGB) colors.
The theory of periodic gratings has been extensively studied in the past. As previously mentioned, light diffraction by periodic phase gratings, whether holographically or acoustically produced, can operate in two different regimes – Bragg or Raman-Nath.
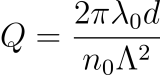
(1)
where, λ0 is the vacuum wavelength of light, d is the grating thickness, Λ is the grating period and n0 is the mean refractive index. Thin gratings are assumed to have values of Q<1, while thick gratings operating in the Bragg regime have values of Q>10. The validity of the parameter Q as a tool for predicting the diffraction regime though has been questioned by several theoretical arguments and experimental observations. Moharam et. al. introduced a different parameter called ‘ρ’ that more accurately determines whether a grating operates in the Raman-Nath or Bragg regimes.

(2)
where δn is the refractive index modulation and the rest of the parameters are similarly defined as for Q. The important difference between these two defined parameters is that ρ does not depend on the thickness of the grating (Eq. 1 and Еq. 2). Therefore, for large grating periods Λ and high index modulation δn (and disregarding the thickness of the grating) higher order diffracted beams become present even for thick gratings. Therefore, when ρ ≫1 the incident beam is only transferred into one diffraction order (Bragg regime), and when ρ ≤1 the incident beam is transferred to multiple orders which correspond to the Raman-Nath regime. As seen in Еq. 2 producing multiple diffracted beams is related to increasing the period of grating and achieving high refractive index modulation.
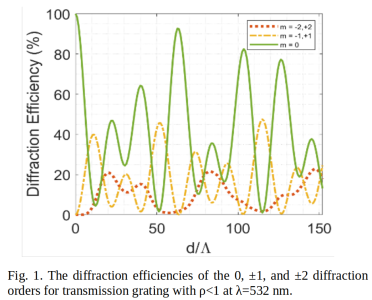
Diffraction to multiple orders in the Raman-Nath regime can be employed to act as a desired multi-channel beam splitter. Therefore, it is essential to optimize the diffraction orders’ relative power, for which we employed numerical RCWA coded in MATLAB. The simulation results for the diffraction efficiency of an un-slanted transmission grating as a function of d/Λ is shown in Fig. 1.
The variation of the diffraction orders’ efficiencies as a function of the incident angle to the grating is depicted in Fig. 2a. It is obvious that the orders’ intensities fluctuate substantially at higher incident angles while at zero incident angle, the diffraction efficiencies of the first 5 diffraction orders are identical (Fig. 2b). Therefore, the incident beam is diffracted to 5 equal-intensity beams and as such this grating performs as a 1 to 5 beam splitter.

For evaluation of the 2D Raman-Nath beam splitter as image multiplicator, a phase light modulator (PLM) made by Texas instrument (TI-DLP670s) was used to generate images.
The PLM encoded a computer-generated hologram (CGH) of the desired image in the beam reflected by it. After diffraction from the gratings, the resulting field was projected in the far field by a lens and as a result, an array of images was constructed as shown in Fig. 3.
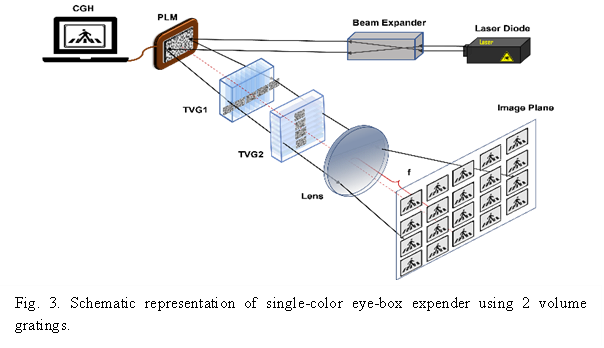
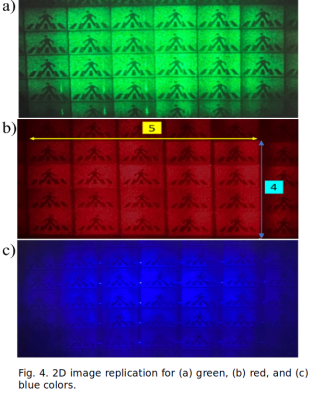
Figure 4 shows the results of 2D beam splitting for the RGB colors. We can conclude that a successful uniform 2D image splitting was achieved by using volume gratings operating not in Bragg but rather in Raman-Nath regime.