Temporal nonlinear dynamics have been studied for more than 40 years in a wide range of domains, from physics to economics to biology [1]. In some cases, observing nonlinear dynamics is seen as a drawback, as it disrupts the steady state of the system. However, in some other cases, nonlinear dynamics are intrinsic to the nominal behavior of the system, for instance in the case of spiking neurons [2]. In large coupled nonlinear systems, the advent of nonlinear dynamics in one component of the system can lead to the propagation of the dynamical features to neighboring components and this is called synchronization. Some standard systems that show synchronizing behavior are metronomes on a common platform, chirping crickets, and clapping audiences. It is now a well-established fact that synchronization in various systems emerges through nonlinear interactions and subsequent dynamics [3]. Synchronization in nonlinear networks is central to many interesting spatiotemporal phenomena, namely, in-phase synchrony, intensity synchronization, time-delayed synchronization, and cluster synchronization [4]. In addition, the time evolution of synchronized networks exhibits diversified behaviors such as periodic or fixed-point behaviors, chaotic synchronization [5], and formation of chimera states [6].
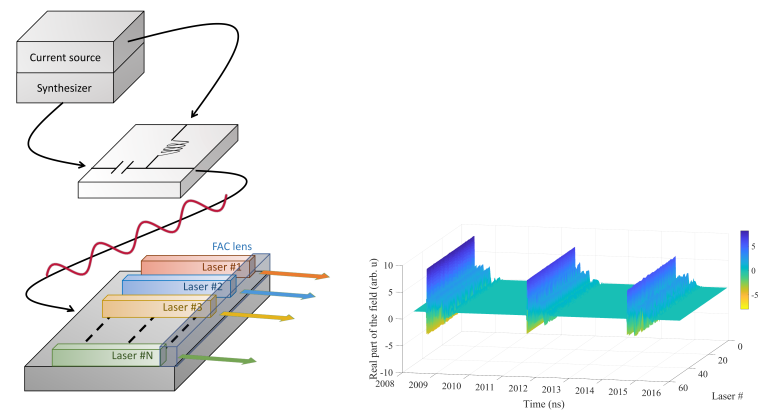
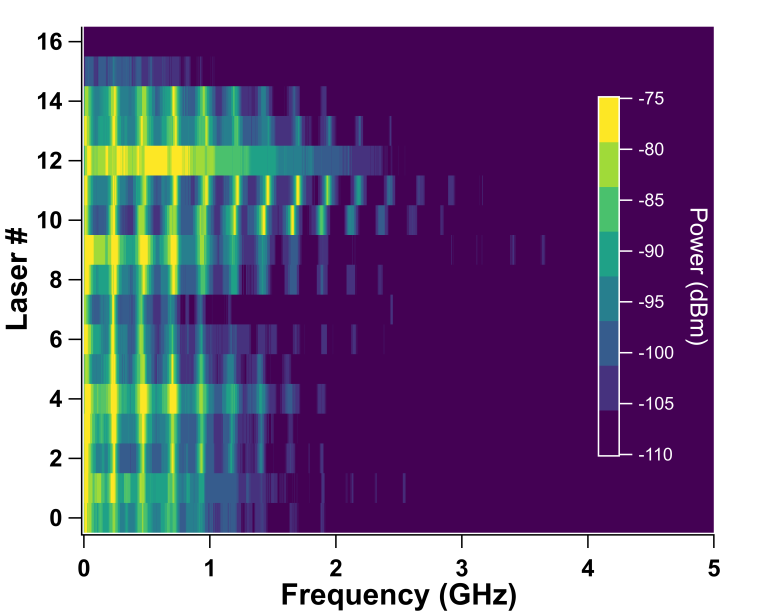
Our team studies nonlinear dynamics and synchronization for two different types of large coupled nonlinear systems, namely diode laser arrays and Josephson junction arrays. For laser diode arrays we have the capabilities to carry out numerical simulations on large arrays of semiconductor lasers made of more than one thousand devices. We also have components made of a few dozens of laser diodes, either in a 1D configuration or in a 2D stack configuration, for conducting experimental research.
Semiconductor diode lasers are reliable nonlinear systems as they are well-tested and verified experimentally [7]. Under the effect of external perturbations (such as those induced by optical feedback and current modulation), semiconductor lasers display a wide variety of nonlinear behaviors and make them a good testing ground for studying nonlinear dynamics, including chaotic behavior. A semiconductor diode array is fundamentally a network of coupled nonlinear oscillators [8]. Due to the nonlinear interaction, phase can be synchronized between nearest-neighbor coupled semiconductor lasers. For systems with two and three lasers, chaotic synchronization is shown to be induced. For a small diode network with two lasers, the stability properties of in-phase and anti-phase synchronization states are well established using the Lang-Kobayashi rate equations and ab-initio coupled mode theory [9]. When the array size is significantly large, the in-phase solutions are destabilized in favor of anti-phase, and travelling-wave solutions. The degree and characteristics of phase synchronization in large semiconductor laser arrays and its dependence on the size of the array remains an open question, especially in the experimental case, thus is the topic of our numerical and experimental research.
Works Cited
1. Strogatz, S. H., [Nonlinear dynamics and chaos: with applications to physics, biology, chemistry and engineering], CRC Press (2018).
2. Montbrio, E., Pazo, D., and Roxin, A., “Macroscopic description for networks of spiking neurons,” Physical Review X 5(2), 021028 (2015).
3. Pikovsky, A., Rosenblum, M., and Kurths, J., [Synchronization: A universal concept in nonlinear science], Cambridge University Press (2002).
4. Dahms, T., Lehnert, J., and Scholl, E., “Cluster and group synchronization in delay-coupled networks,” Physical Review E 86(1), 016202 (2012).
5. Pecora, L. M., and Carroll, T. L., “Synchronization in chaotic systems,” Physical Review Letters 64(8), 821 (1990).
6. Hart, J. D., Bansal, K., Murphy, T. E., and Roy, R., “Experimental observation of chimera and cluster states in a minimal globally coupled network,” Chaos: an Interdisciplinary Journal of Nonlinear Science 26(9), 094801 (2016).
7. Lang, R., and Kobayashi, K., “External optical feedback effects on semiconductor injection laser properties,” IEEE Journal of Quantum Electronics 16(3), 347-355 (1980).
8. Soriano, M. C., Garcia-Ojalvo, J., Mirasso, C. M., and Fischer, I., “Complex photonics: dynamics and applications of delay-coupled semiconductor lasers,” Reviews of Modern Physics 85(1), 421 (2013).
9. Adams, M., Li, N., Cemlyn, B., Susanto, H., and Henning, I., “Effect of detuning, gain guiding and index antiguiding on the dynamics of two laterally coupled semiconductor lasers,” Physical Review A 95(5), 053869 (2017).