Topics
Scalable phase-locking and synchronization in laser diode arrays
Semiconductor laser diodes are employed for a wide variety of applications. Such lasers can emit light at a wide range of wavelengths, exhibit high electro-optical efficiency, are compact, and are low cost. However, a single diode’s emission power is in the range of Watts or lower. Assembling diode lasers in arrays has the potential to increase emission brightness while keeping high-power diode array operation. We are studying the mechanisms of spontaneous and scalable phase-locking, both experimentally and theoretically. These studies involve designing and experimentally demonstrating compact external cavity design that fosters coupling between the diodes, consequently resulting in diode array synchronization.
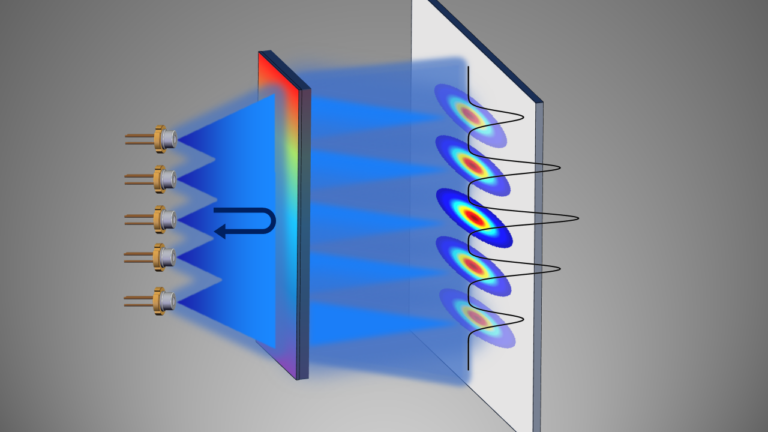
Our team studies nonlinear dynamics and synchronization of large coupled systems, focusing on semiconductor diode laser arrays. Such lasers display a wide variety of nonlinear behaviors making them a good testing ground for studying nonlinear dynamics, including chaotic behavior.
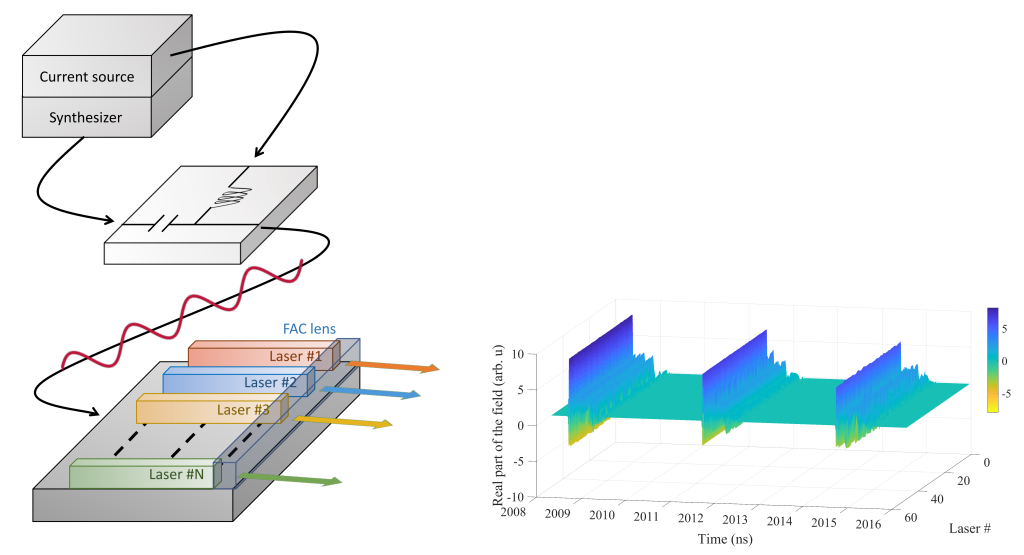
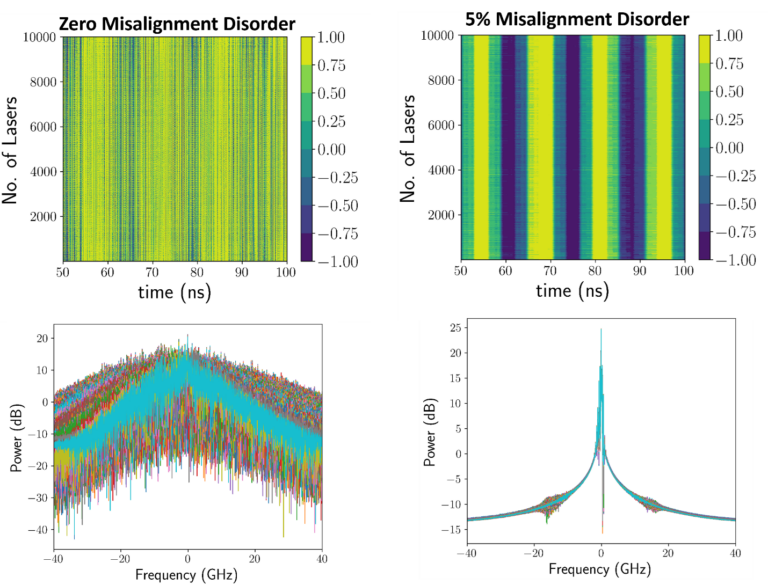
The realization that heterogeneity in complex system parameters (disorder) can promote synchronization broadens our understanding of complex systems. It challenges the simplistic view that order always leads to order and has implications for designing and understanding various real-world systems like large-scale laser arrays that are of interest to the scientific community. Our research investigates disorder-promoted synchronization (DPS) in large-scale nonlinear oscillator arrangements and other physical settings, such as coupled diode laser arrays, arrays of coupled Josephson junctions and coupled nonlinear oscillators.
Our group is developing methods for detecting weak signals in noisy environments using nonlinear dynamics methods. Our developed novel methodology is based on nonlinear systems described by coupled differential equations and is a sound candidate for detecting signals with low signal-to-noise ratios (SNRs). This research focuses on numerical and analytical efforts and takes advantage of the strong computational resources that we have.
